F (x) = 1 f ( x) = 1 Rewrite the function as an equation y = 1 y = 1 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x bThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}\left (f4\right)x5=0 x2 (∣f ∣ − 4) x − 5 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, f4 for b, and 5 for c in the quadratic formula, \frac {For each x x value, there is one y y value Select few x x values from the domain It would be more useful to select the values so that they are around the x x value of the absolute value vertex Tap for more steps Substitute the x x value − 1 1 into f ( x) = x − 1 f ( x) = x 1 In this case, the point is ( − 1, 2) ( 1, 2)
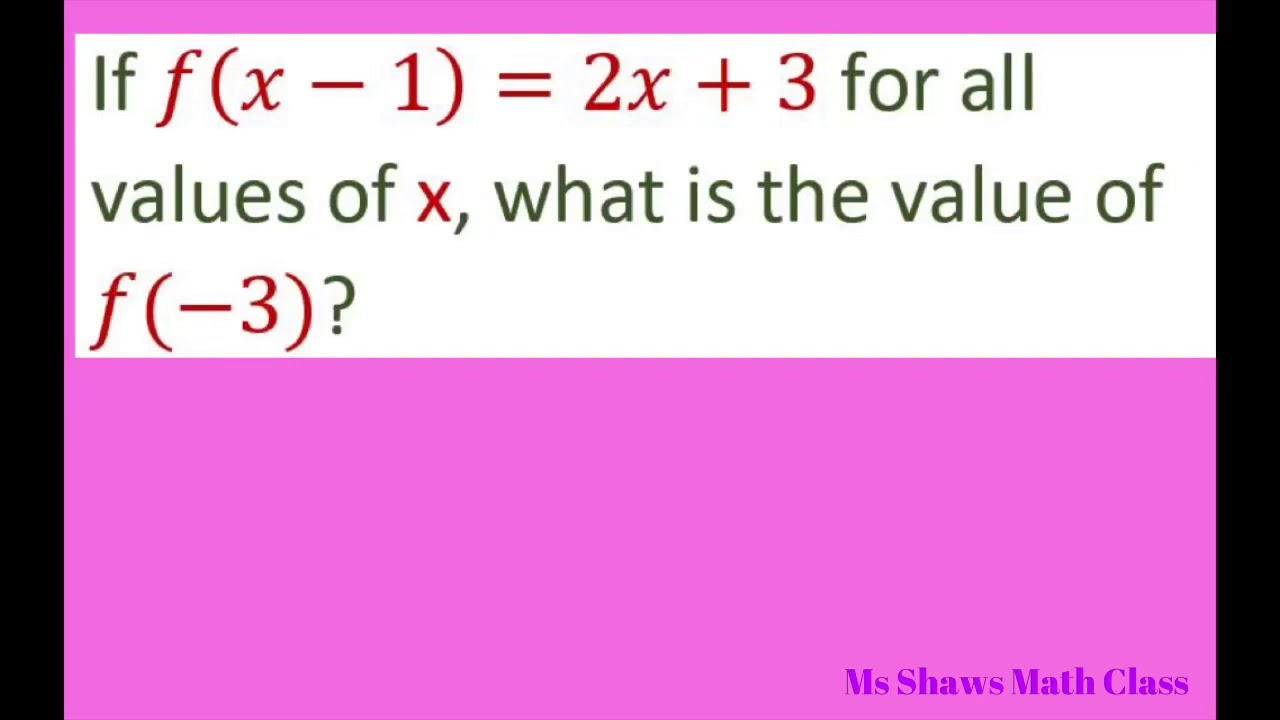
If F X 1 2x 3 Find F 3 Youtube
F(x) = x/1+x2
F(x) = x/1+x2-The maximum occurs where the denominator x^2 2 is at a mininum Clearly, x^2 2 must have a minimum of 2, because x^2 is either 0 or positive So the maximum value of f(x) is 1/2, and occurs at x = 0 On the other hand, there is no minimum, becThe known derivatives of the elementary functions x 2, x 4, sin(x), ln(x) and exp(x) = e x, as well as the constant 7, were also used Definition with hyperreals Relative to a hyperreal extension R ⊂ ⁎ R of the real numbers, the derivative of a real function y = f ( x ) at a real point x can be defined as the shadow of the quotient ∆ y / ∆ x for infinitesimal ∆ x , where ∆ y = f



F X X 2
G(x) = (2x) 2 C > 1 compresses it;Note that (unlike for the ydirection), bigger values cause more compression We can flip it upside down by multiplying the whole function by −1 g(x) = −(x 2) This is also called reflection about the xaxis (the axis where y=0) We can combine a negative value with a scalingSteps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1
Misc 4 Show that function f R → {x ∈ R −1 < x < 1} defined by f(x) = x/(1 𝑥 ) , x ∈ R is oneone and onto function f R → {x ∈ R −1 < x < 1Precalculus Functions Defined and Notation Function Composition 1 AnswerAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
Divide 0 0 by 4 4 Multiply − 1 1 by 0 0 Add − 1 1 and 0 0 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e Set y y equal to the new right side Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k kFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 f (x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domainDetermining f 1 (x) of functions You write the inverse of \(f(x)\) as \({f^{ 1}}(x)\) This reverses the process of \(f(x)\) and takes you back to your original values Example



More Differentiation By First Principles




1 Najdite F 0 Esli F X X 2 3 X 1 2 Najdite A F X B F 64 Esli F X 6 X Shkolnye Znaniya Com
1 Introduction The composition of two functions g and f is the new function we get by performing f first, and then performing g For example, if we let f be the function given by f(x) = x2 and let g be the function given by g(x) = x3, then the composition of g with f is called gf and is worked outFind the inverse of f(x) = 2x 1 Let y = f(x), therefore y = 2x 1 swap the x"s and y"s x = 2y 1 Make y the subject of the formula 2y = x 1, so y = ½(x 1) Therefore f 1 (x) = ½(x 1) f1 (x) is the standard notation for the inverse of f(x) The inverse is said to exist if and only there is a function f1 with ff1 (x) = f1 f(x) = xBecause f takes arbitrarily large and arbitrarily small positive values, any number y > 0 lies between f(x 0) and f(x 1) for suitable x 0 and x 1 Hence, the intermediate value theorem ensures that the equation f ( x ) = y has a solution



Find F 1 If F X X 1 2x 2 7x 5 When X 1 F X 1 3 When X 1 Sarthaks Econnect Largest Online Education Community



Let F R R Be The Function Defined By F X 1 2 Cos X Sarthaks Econnect Largest Online Education Community
Simple and best practice solution for F(x)=(x1)(x3) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSummary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functions Range is the set of values of the dependent variable used in the function f (x) for which f (x) is defined Hence, Range f (x) ≥ 0 Interval Notation 0,∞) Step 3 Additional note The function y = f (x) = √x −1 has no asymptotes Create a data table using values for x and corresponding values for y Observe that Zero and Negative



F X 1 Cos Kx X Sin X If X 0 At X 0 1 2 If X 0 Studyrankersonline



Quantitative Aptitude Algebra Functions If F X 2 F X F X 1 Handa Ka Funda Online Coaching For Cat And Banking Exams
Putting f(x1) = f(x2) we have to prove x1 = x2 1/x1 = 1/x2 x2 = x1 x1 = x2 Hence, if f(x1) = f(x2) , x1 = x2 ∴ f is oneone Check onto f N → R* f(x) = 1/x Let y = f(x) , , such that y ∈ R* y = 1/𝑥 x = 1/𝑦 Since y is real number except 0, x cannot always be a natural number Example Let y = 2 x = 1/2 So, x is not a natural number Hence, f is not ontoAlgebra 1 How to find f(x) Study concepts, example questions & explanations for Algebra 1 CREATE AN ACCOUNT Create Tests & Flashcards Home Embed All Algebra 1 Resources 10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn byNotice that the main points on this graph are \(x = 2,\,1,\,4\) Graph of y = f(x) k Adding or subtracting a constant \(k\) to a function has the effect of shifting the graph up or down




Example 9 Discuss Continuity Of F X 1 X Chapter 5




Example Show That Function F X 1 X X Is Continous
0 < C < 1 stretches it;Subtract $ fe^x $ from both sides, factorize the resulting LHS as $ f (1e^x) $ and divide both sides through by $(1 e^x) $ $\endgroup$ – Frank Apr 2 '14 at 1234 Add a comment 1 How do you find the inverse of #f(x)=(x1)/(x2)# and graph both f and #f^1#?




If The Function F X X 2 1 X 1 When X 1 K When X 1




The Range Of F X X 1 X Is
Or e x can be defined as f x (1), where f x R → B is the solution to the differential equation df x / dt (t) = x f x (t), with initial condition f x (0) = 1; f '(x) = 2x2 4x k Now let's evaluate f '(x), when x = − 1, knowing that the result f '(−1) is equal to 1, as stated in the problem f '(− 1) = 2 ⋅ 1 4 ⋅ (−1) k = −2 k −2 k = 1 See the explanation below If a function f(x) has an inverse f^1(x) then The composition f(f^1(x))=x and f^1(f(x))=x Here, we have f(x)=1x^3 g(x)=root(3)(1x) Then




If The Function F R R Defined By F X 4 X4 X 2 Then Show That F 1 X 1 F X And Hence Deduce The Value Of F 14 2f 12 F 34




Pust F X X 2 X 1 Pri Kakih Znacheniyah H A F X Gt 0 B F X 0 V F X Lt 0 V Shkolnye Znaniya Com
It follows that f x (t) = e tx for every t in R1 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of y = x2 is a parabola) y xExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Let F X 6 X And Let G X X X 1 Find F O G F O Chegg Com




Find The Fourier Sine Transform Of F X 1 X Mathematics 3 Question Answer Collection
F(x) = 1/x, g(x) = 1/xDivide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect squareAs you can see, this function is split into two halves the half that comes before x = 1, and the half that goes from x = 1 to infinity Which half of the function you use depends on what the value of x is Let's examine this Given the function f (x) as defined above, evaluate the function at the following values x = –1, x = 3, and x = 1




Inverse Of A Function In Math Tutorial Explaining Inverses Step By Step Several Practice Problems Plus A Free Worksheet With Answer Key




Misc 4 Find Domain And Range Of F X Root X 1 Chapter 2
∫ f (x)dx = ∫ ln(x)dx = x ∙ (ln(x) 1) C Ln of 0 The natural logarithm of zero is undefined ln(0) is undefined The limit near 0 of the natural logarithm of x, when x approaches zero, is minus infinity Ln of 1 The natural logarithm of one is zero ln(1) = 0 Ln of infinity The limit of natural logarithm of infinity, when xExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicSo, for the function f(x) = 1/x the yaxis is a vertical asymptote, and the xaxis is a horizontal asymptote In the following diagram of this function the asymptotes are drawn as white lines The function f(x) = 1/x is an excellent starting point from which to build an understanding of rational functions in general
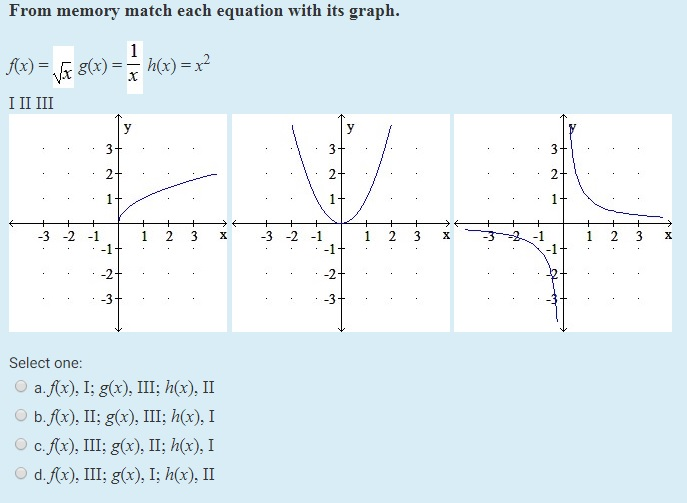



From Memory Match Each Equation With Its Graph Chegg Com



What Is The Inverse Of The Function F X X X 1 Quora
Fxgx=x\sqrt {x1} f x g x = x x − 1 Subtract gx from both sides Subtract g x from both sides fx=x\sqrt {x1}gx f x = x x − 1 − g x The equation is in standard form The equation is in standard form xf=gxx\sqrt {x1}In simple terms, that notation implies that f^1(x) is the Inverse Function to f(x) To make is a bit easier to wrtie, let's let g(x) be the inverse of f(x), in other words, g(x) = f^1(x) In terms of mappings, If D is the domain of f and R is theFor all x and y such that −1 < x < 1 (otherwise the denominator f X (x) vanishes) and < < (otherwise the conditional probability degenerates to 0 or 1) One may also treat the conditional probability as a random variable, — a function of the random variable X , namely,




If F X 1 2x 1 X 1 2 Then Show That F F X 2x 1 2x 3 Provided That X 3 2dot




How Do You Find F X Using The Limit Definition Given F X X 2 1 2x 3 Socratic
1 cf(x) (a,b) 7!(a, 1 cb) shrink vertically by 1 c f(x) (a,b) 7!(a,b) flip over the xaxis Examples • The graph of f(x)=x2 is a graph that we know how to draw It's drawn on page 59 We can use this graph that we know and the chart above to draw f(x)2, f(x) 2, 2f(x), 1 2f(x), and f(x) Or to write the previous five functionsIf f is such a function, then g ( x) = sin 2 ( π f ( x) 2) is also such a function If f ( 1) = 0, take g ( x) = sin ( f ( x)) So you will really need much stronger restrictions than infinite differentiability etc As to your edit, continuity is enough We can first show f ( 1 / q) = f ( 1) / q for integral qLet x and y be any two elements in the domain (N), such that f(x) = f(y) ⇒ `x^2 x 1 = y^2 y 1` ⇒ `(x^2 y^2 ) (x y ) = 0 ` ⇒ (x y) (x y ) (xy ) = 0 ⇒ ( x y) ( x y 1) = 0 ⇒ x y = 0 x y 1 can not be zero because x and y are natural numbers ⇒ x =y So, f is oneone Surjectivity when x = 1 `x^2 x 1




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot



Find The Value Of A If The Function F X Defined By F X 2x 1 X 2 And A X 2 And X 1 X 2 Is
Free graphing calculator instantly graphs your math problemsF(x) is not a onetoone function, and has no inverse function with its natural domain、 But the inverse RELATION of the relaton y=x(1/x) is the relation x=y(1/y) If Df=1,∞)=Rf^(1)→Rf=2,∞ let f^1(x)=u f(u)=x=(u²1)/u ux=u²1 u²xu1=0 f^1The values of the function ( y values ) in the table of values for f(x) = x 2 1 are all one higher than the corresponding values in the table of values for g(x) = x 2 and the graph has been translated vertically by 1 unit Note that the grah of f(x) = x 2 1 does not cross the x axis This tells us that the equation x 2 1 = 0 has no solution We know this already as a squared number is



F X X 2 Graph




Exercise 1 3 Functions Problem Questions With Answer Solution
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeA specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write "5x" instead of "5*x" The Derivative Calculator has to detect these cases and insert the multiplication sign The parser is implemented in JavaScript, based on the Shuntingyard algorithm, and can run directly in the browserQuadratic polynomial can be factored using the transformation a x 2 b x c = a (x − x 1 ) (x − x 2 ), where x 1 and x 2 are the solutions of the quadratic equation a x 2 b x c = 0 x^{2}3x5=0




If F X F X Is A Differentiable Function And G X G X Is A Double Differentiable Function Such That F X 1 F X 1 And F 39 X G X F X G X If F2 0 G2 0 9f2 Mathematics Topperlearning Com Vf5dz0tt




Prove Function Series F N X Sin X 1 N Doesn Converge Uniformly Mathematics Stack Exchange
Let f(x) = x 2 3 g(x) = 2x 1 Q2) Find fg(x) and explain why fg(x) = 1 has no real solution Like in Q1) we must find the function fg(x) before we solve it fg(x) = fg(x) = f(2x1) = (2x1) 2 3 If we follow the same method as before we will find that fg(x) = 1 has no real solution fg(x) = (2x1) 2 3 = 1Therefore f(f − 1(x)) = f(y) = x A function f has an inverse function f − 1, iff f is bijective Let f A → B, such that f(x) = y, with x ∈ A, y ∈ B Then its inverse is a function such that f − 1 maps from the codomain of f to the domain of f, this is f − 1 B → A So, ∀y ∈ B, f − 1(y) = x, with x ∈ A Explanation Your function is defined for any value of x except the value that will make the denominator equal to zero More specifically, your function 1 x will be undefined for x = 0, which means that its domain will be R − {0}, or (− ∞,0) ∪ (0, ∞)



Rational Function F X 1 X Zona Land Education



How To Find Inverse Function Of X 1 X Given That F X Is Bigger Or Equal To 2 Quora



F X 1 Kx 1 Kx X If 1 X 0 At X 0 2x 1 X 1 If 0 X 0 Studyrankersonline



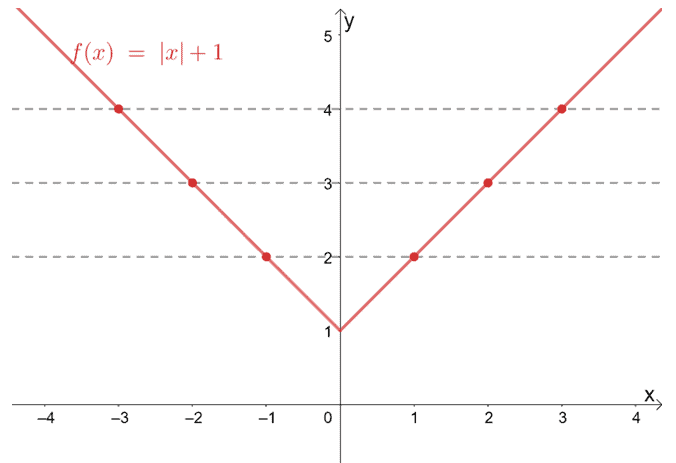
1
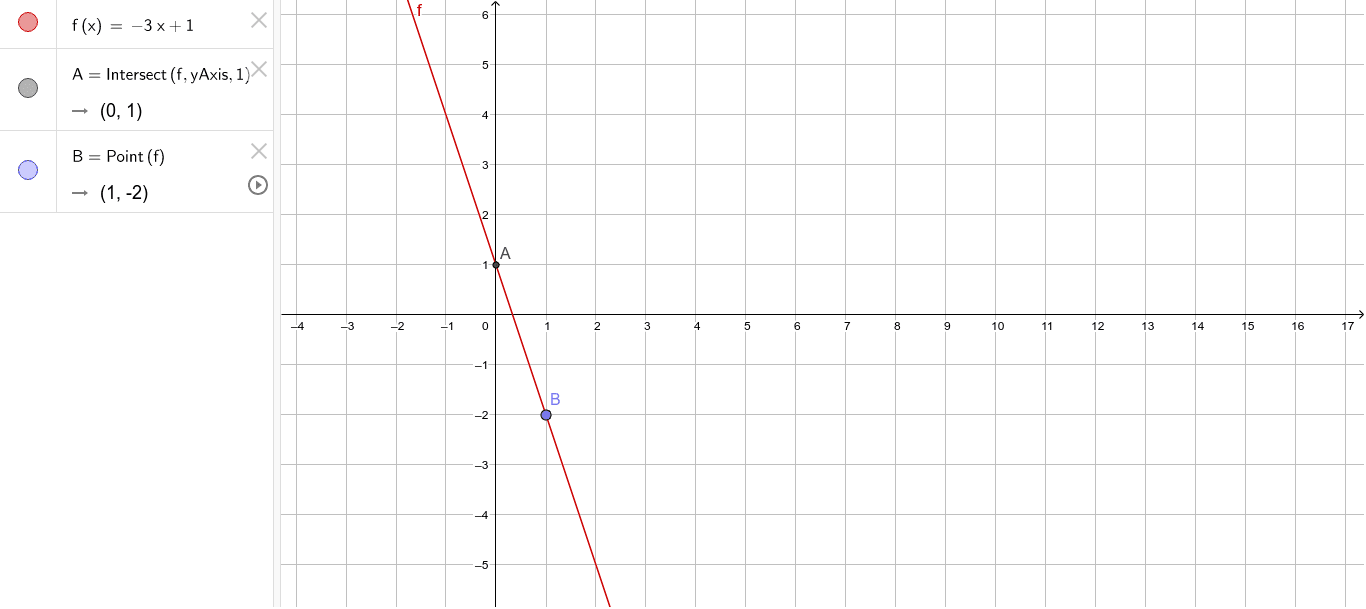



F X 3x 1 Geogebra




If F X X 1 X 1 Then Show That F 1 X F X Ii F 1 X 1 F X




Exercise 1 5 Composition Of Functions Problem Questions With Answer Solution Mathematics




7 Find The Fourier Series Of The Given Function A F X 1 P X P B F X 0 2 Ke 0 X 1 1 X 0 1 1 X 0 F X
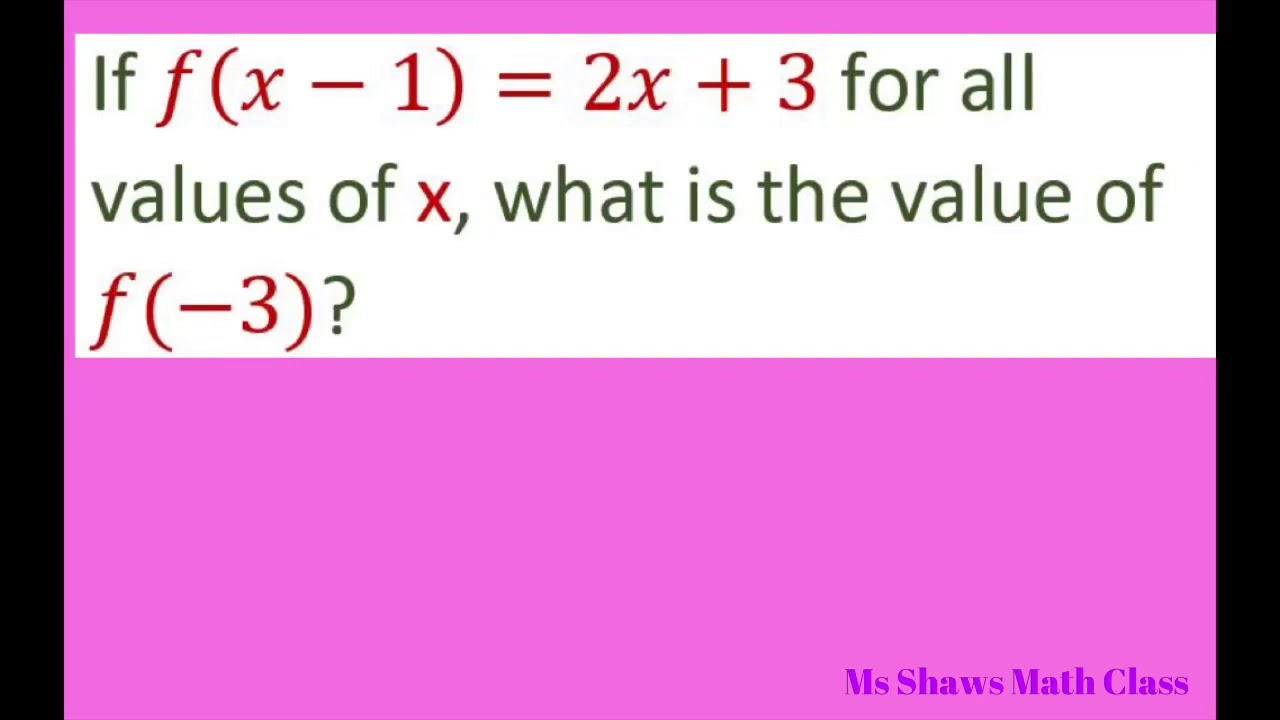



If F X 1 2x 3 Find F 3 Youtube




How Do You Find F X Using The Definition Of A Derivative For F X 4 X 1 4x Socratic




If F X 2f 1 X X 2 2 X R Then F X Is Given By




If F X X 3 1x 3 Show That F X F 1x 0



Schaubild F X 2x 1 5 Und F X 1 5x Mathelounge
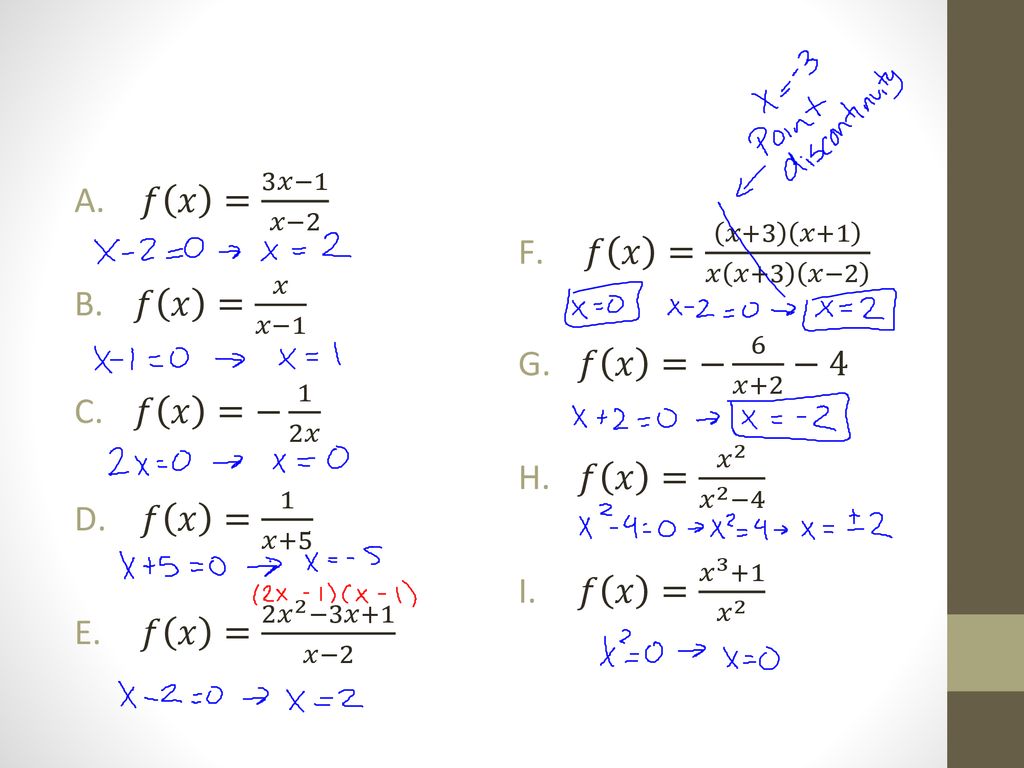



3 7 Graph Of Rational Functions Ppt Download




Let The Function F Be Defined By F X 2x 1 1 3x Then F 1 X Is




Ex 5 1 5 Is F X X X 1 5 X 1 Continuous At X 0 1 2




Four Ways To Define A Function 1 1 Functions
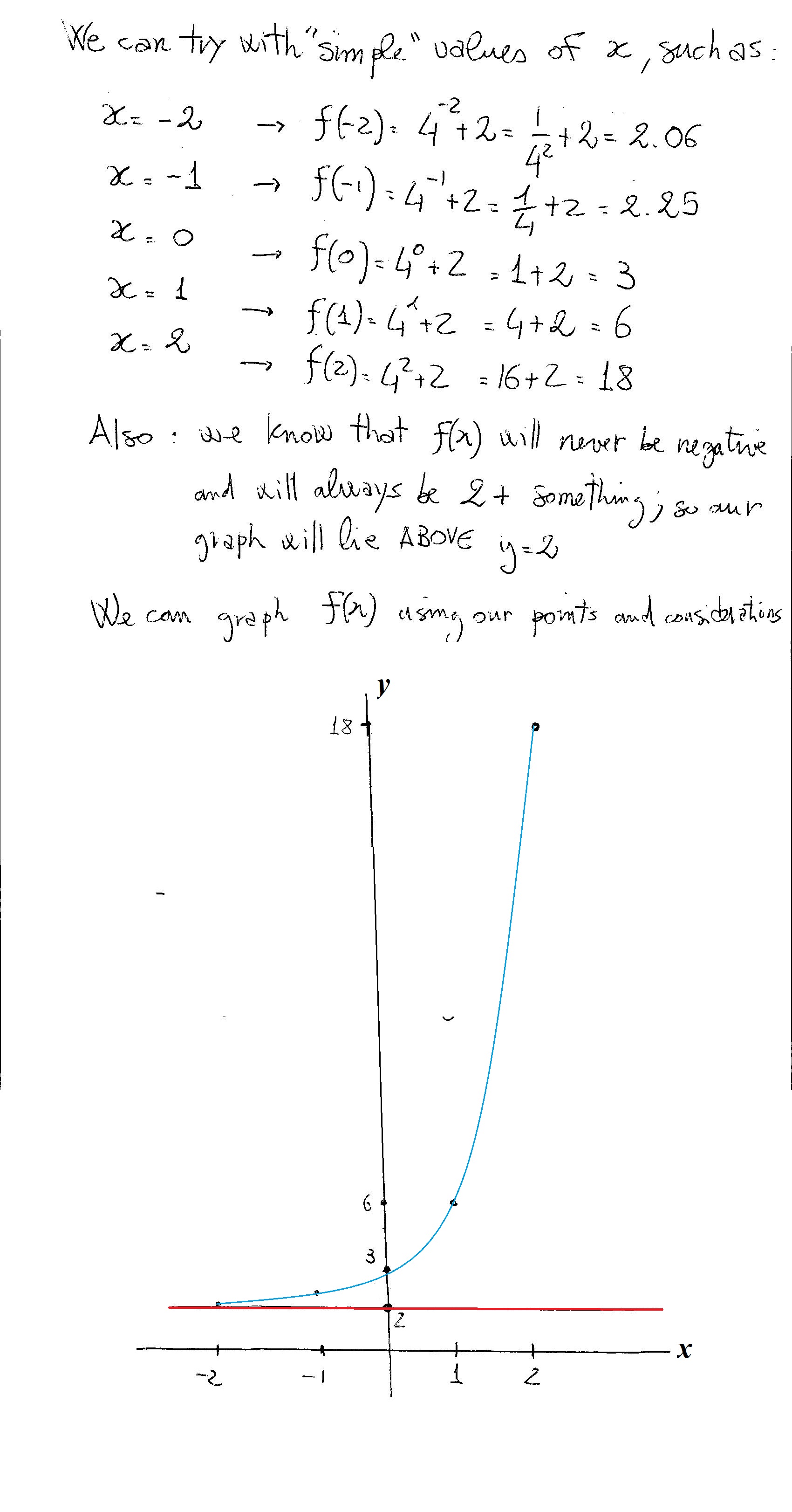



How Do You Graph The Exponential Function F X 4 X 2 Socratic




Misc 7 Let F X X 1 G X 2x 3 Find F G F G F G




If F X F 1 X F X F 1 X And F 3 28 Then Find F 4 Youtube
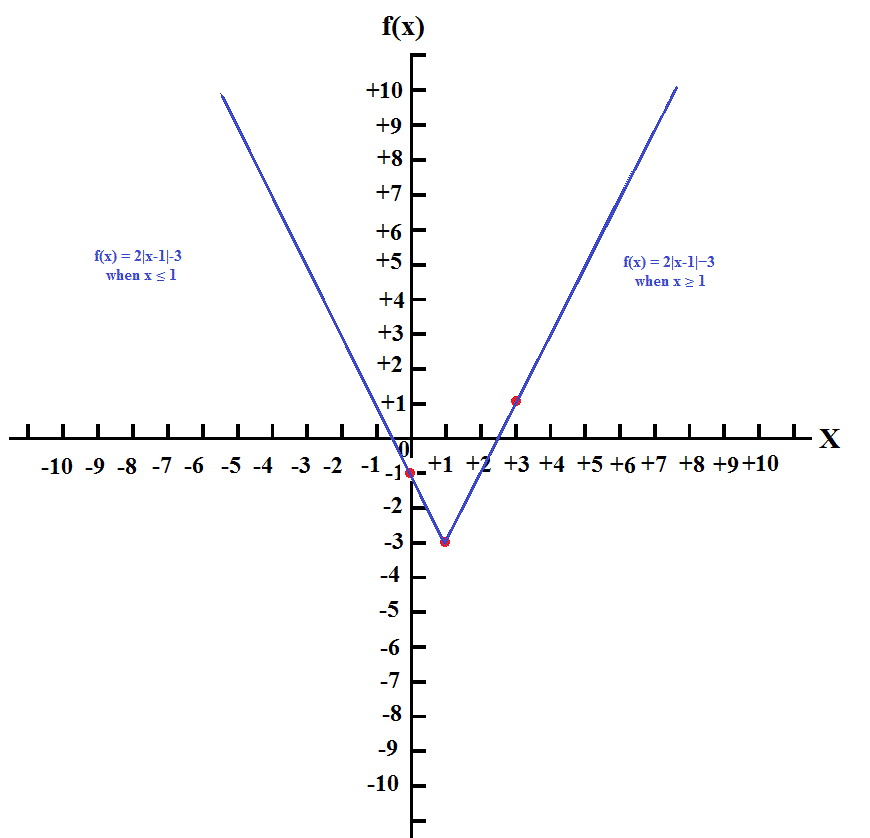



How Do You Graph F X 2abs X 1 3 Socratic
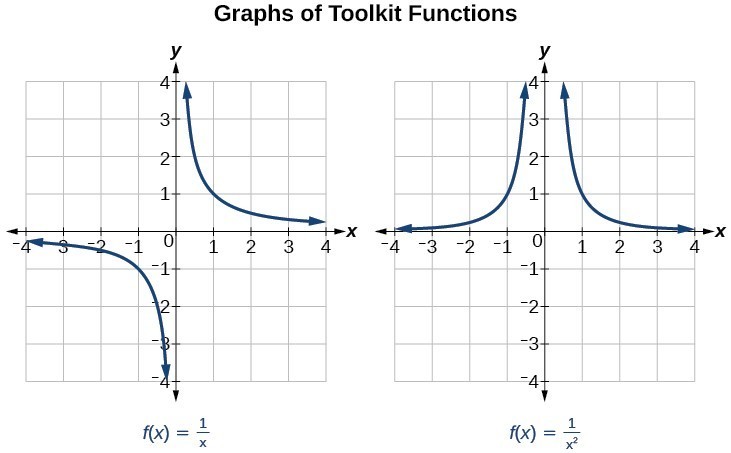



Characteristics Of Rational Functions College Algebra




Rd Sharma Class 12 Solutions Updated For 21 22 Chapter 18 Maxima And Minima




If F X X 1 X 1 Then Find F X F 1 X Brainly In




Find The Fourier Sine Transform Of F X 1 X Mathematics 3 Question Answer Collection



One To One Function Explanation Examples




How To Tell If A Function Is Even Or Odd 8 Steps With Pictures
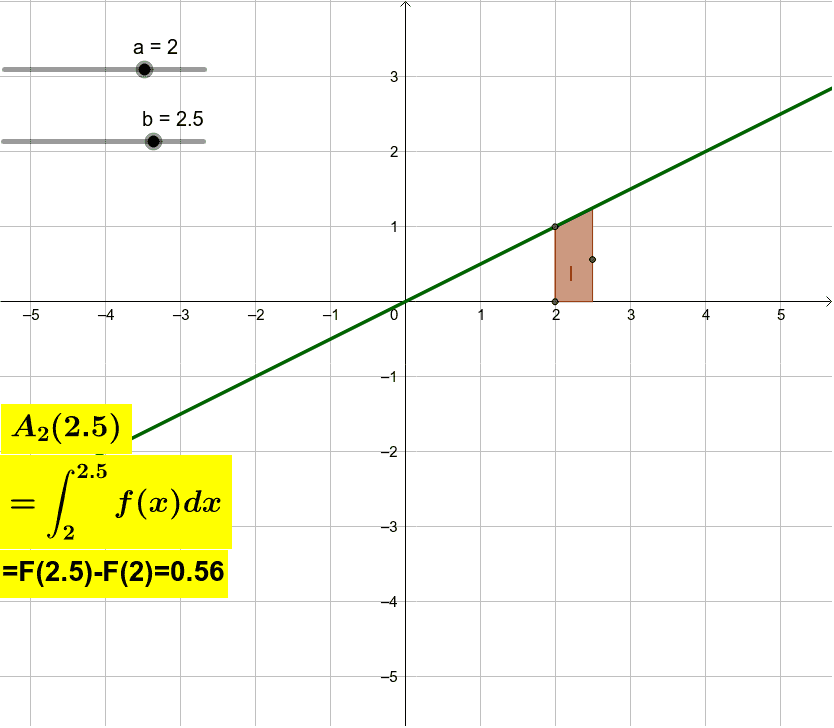



F X 1 2x Geogebra
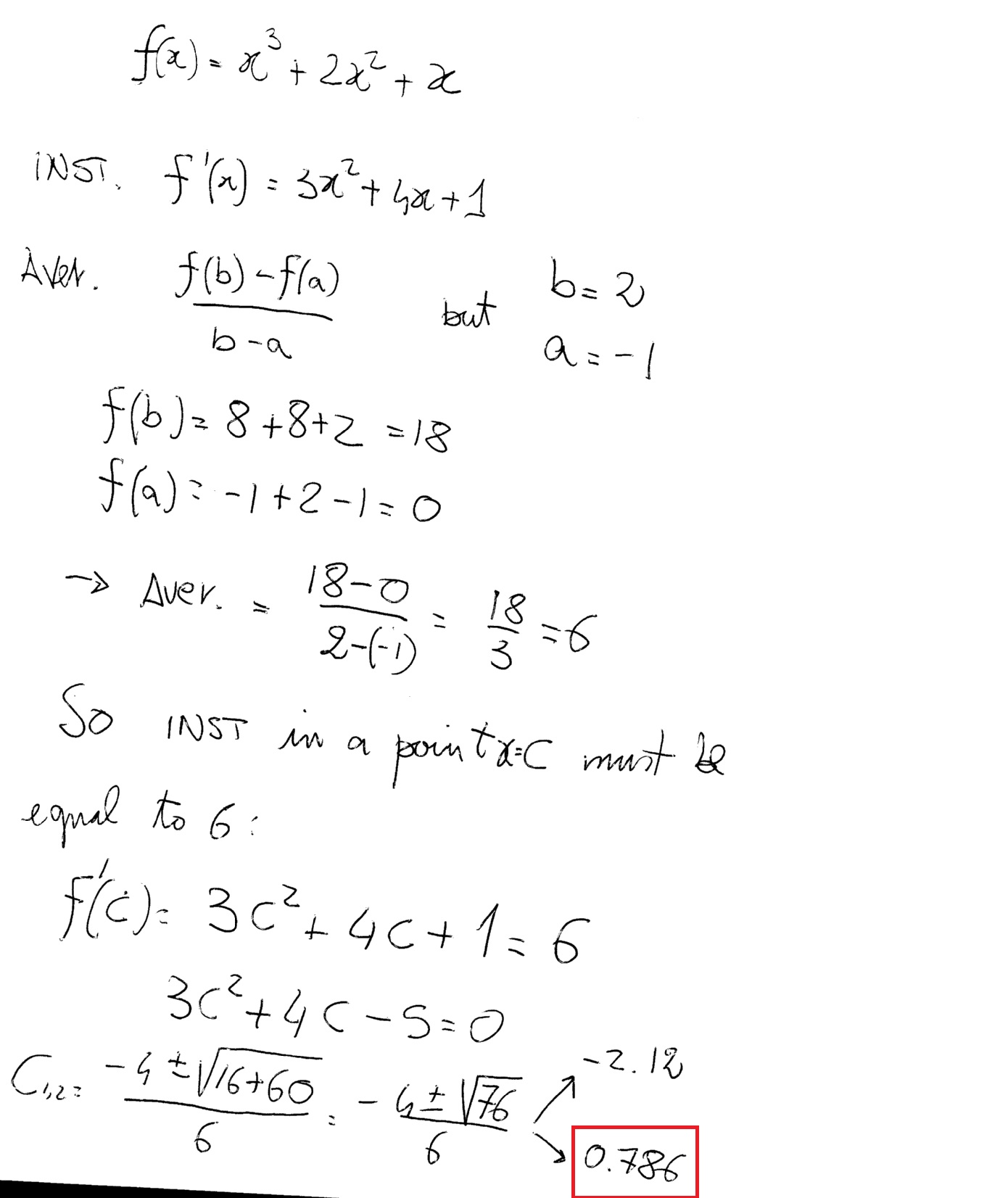



If F Is Defined By F X X 3 2x 2 X How Do You Find The Value Of X When The Average Rate Of Change Of F On The Interval X 1 To X




If F X X 1x 1 Then F 2x In Terms Of F X Is




Misc 4 Show F X X 1 X Is One One Onto Miscellaneous
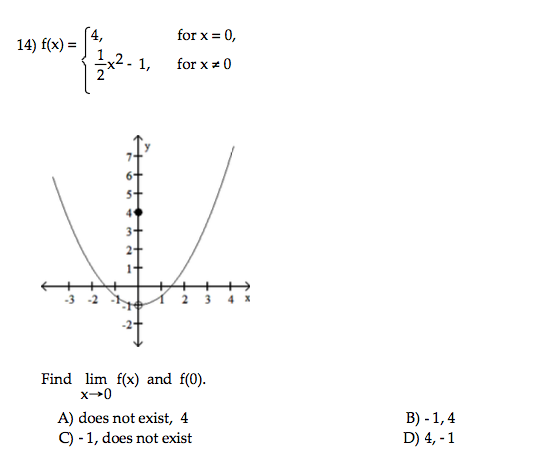



F X 4 For X 0 1 2 X 2 1 For X Notequalto 0 Chegg Com




For The Function Defined By F X X 2 X Less Than Equal To 1 2x 1 X Greater Than 1 Define F 0 And Also Draw The Graph For F X Study Com



Math Scene Equations Iii Lesson 3 Quadratic Equations




How To Algebraically Find The Inverse Of A Function 5 Steps




If F X X 1 X 1 Prove Fof 1 X X




What Is The Difference Between F X 1 Geq F X 2 And F X 1 F X 2 Mathematics Stack Exchange




How To Solve Questions As If F X X 1 X 1 Then Show That F F X Equals To Minus One Upon X Maths Relations And Functions Meritnation Com
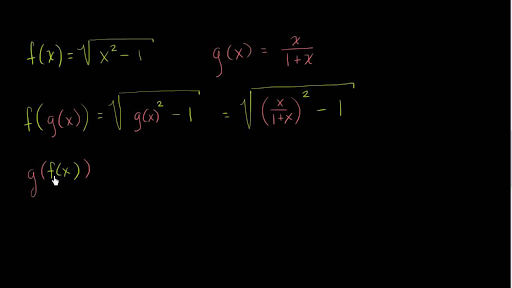



Finding Composite Functions Video Khan Academy




If F X 1 X X 3 X 3 Then F 5 Must Be Equal To
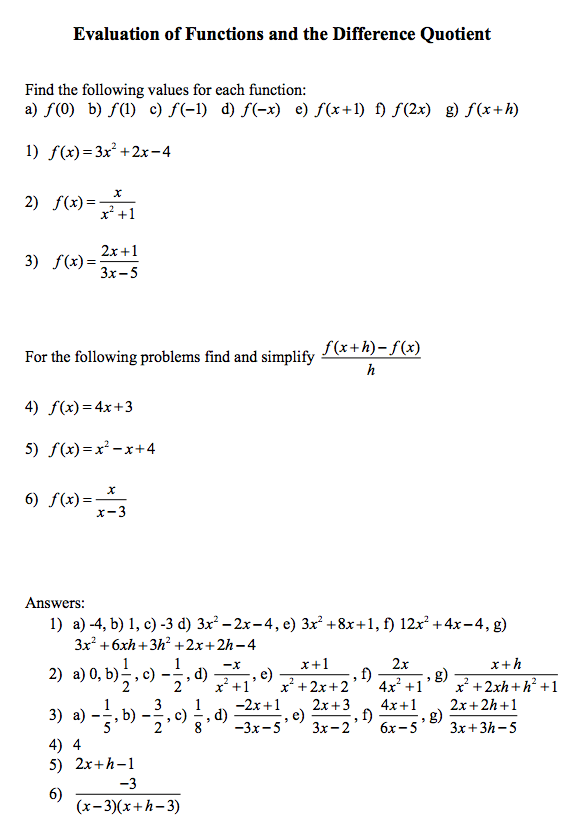



Find The Following Values For Each Function A F 0 Chegg Com




Asymptote Wikipedia



F X X 2




If F X X3 1 X3 Prove That F X F 1 X 0 Brainly In




Find The Domain And Range Of The Real Function Fx 1 1 X 2 Brainly In




Finding Inverse Functions Quadratic Example 2 Video Khan Academy



Www Topperlearning Com Answer Let F X Ax X 1 X Is Not Equal To 1 Then For What Value Of A Is F F X X Sehzhdzz




7 Modified Newton Raphson Method



Find The Root Of Nbsp X3 X 1 0 Correct To Four Decimal Places Usinnewton Raphson Method
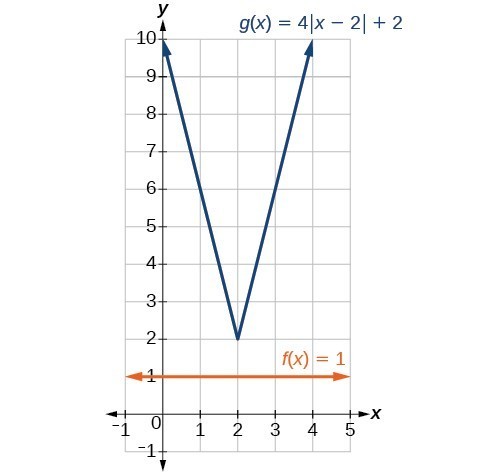



Solve An Absolute Value Equation College Algebra



Math Scene Equations Iii Lesson 3 Quadratic Equations
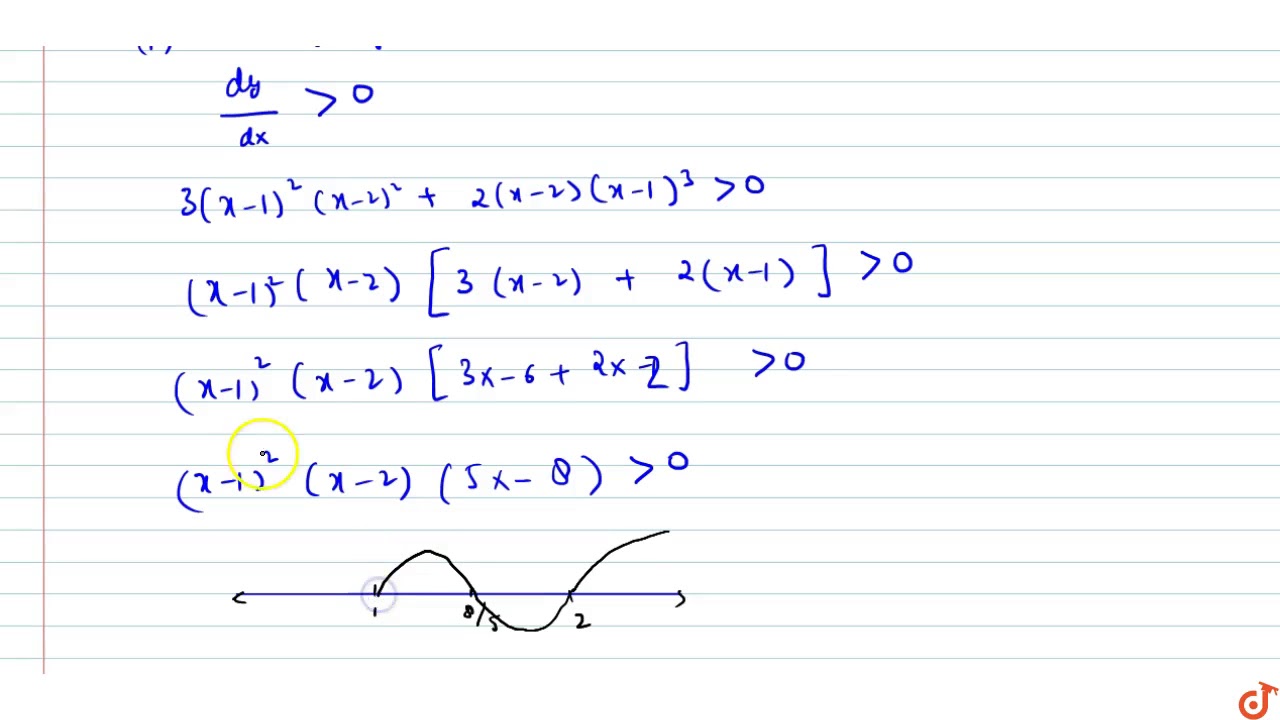



Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube




If F X X 1 X 2 X 3 Then A Maximum Value Of F X Is 3 If X In 2 3 B Maximum Youtube



Discuss Continuity Of The Function F Given By F X X 1 X 2 At X 1 And X 2 From Mathematics Continuity And Differentiability Class 12 Cbse




How To Find The Domain Of F X X 1 X 2 X 3 X 4 Quora




Solution If F X 1 1 X 2 Then What Is F X



Bitte Um Zeichnung Der Linearen Funktion F X 1 Mathelounge




Wie Zeichne Ich Den Graph Zu Der Funktion F X 1 X Also 1 Durch X Mathematik




5 4 Exponential Functions Differentiation And Integration The Inverse Of F X Ln X Is F 1 E X Therefore Ln E X X And E Ln X X Solve For Ppt Download




If F X X 1 X And F 1 5 2 Then F X Brainly In




Let F X 0 If X Lt 0 X If 0 X 1 2 X If 1 Chegg Com



If The Periodic Function F X Satisfies The Equation F X 1 F X 1 3 F X X R Then Find The Period Of F X Sarthaks Econnect Largest Online Education Community



Www Jstor Org Stable



F X 1 X 2 Graph




F X X X X Not Equal To 0 And 1 X 0 Is The F X Is Continuous Mathematics Topperlearning Com Qg0xnj33




Consider F X X 2 X 0 X 1 For X 1 For X 1 Chegg Com




If F X 2x 1 If X Gt 1 And X 2 1 If 1 Lt X Lt 1 And If F 1 F 3 F X F 2 F Youtube




Transformations Of The 1 X Function Video Lesson Transcript Study Com



Asymptote A Linear Boundary That A Curve Gets Very Close To But Never Reaches



Solution Sketch F X X 1 If X Lt 1 0 If 1 Amp 04 X Amp 04 1 X 1 If X Gt 1 Find The Domain And Range Using Interval Notation




Is The Function F Defined By F X X If X 1 5 If X 1 Continuous At X 0 At X 1 At X 2 Mathematics Shaalaa Com




Find The Range Of F X 1 4 X 2
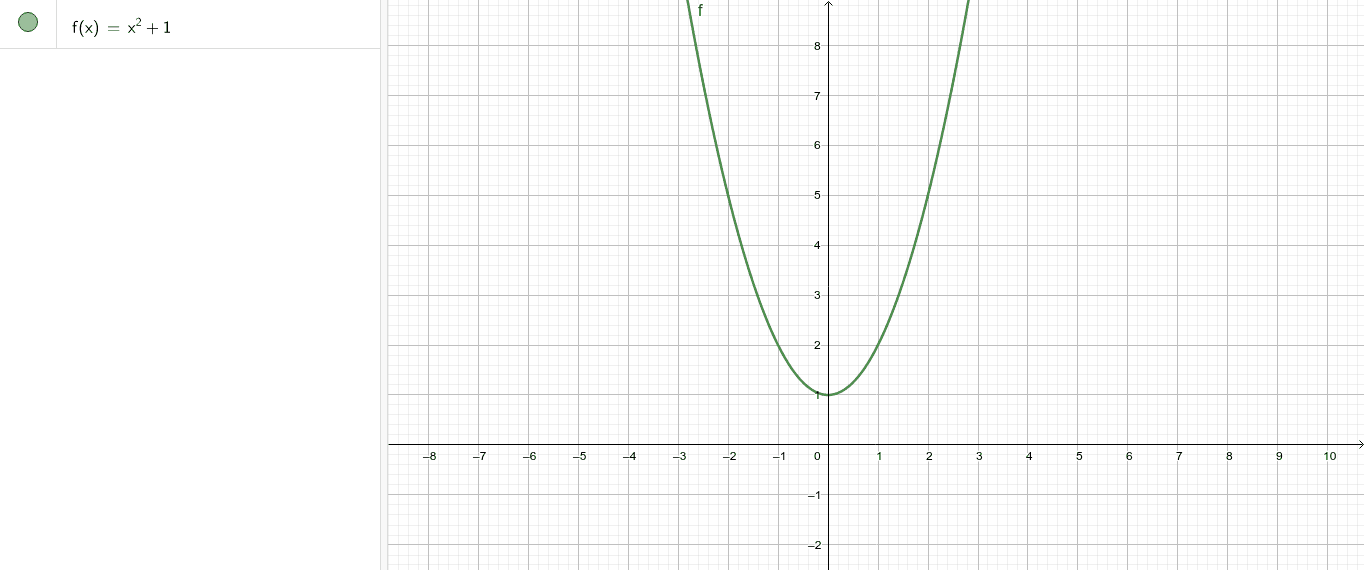



F X X2 1 Geogebra



What Is The Range Of The Function F X X 1 X 1 Sarthaks Econnect Largest Online Education Community
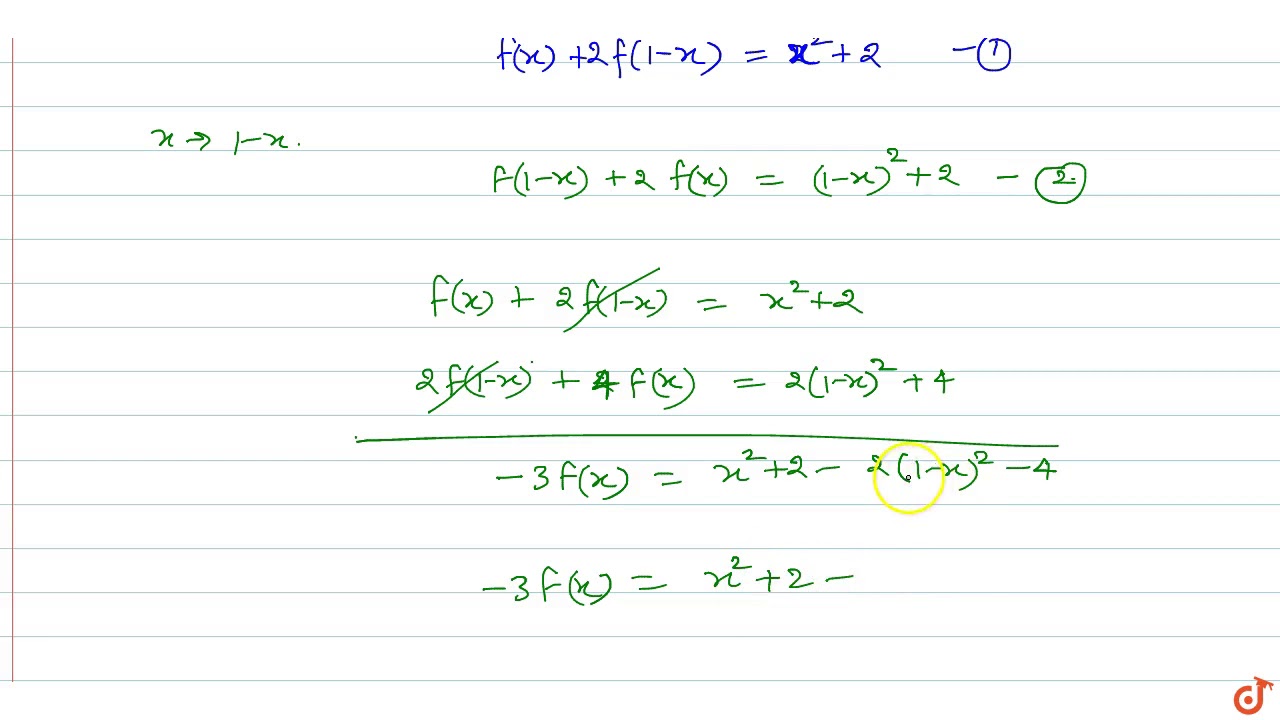



If F X 2f 1 X X 2 2aa X In R Then F X Given As Youtube




Misc 4 Show F X X 1 X Is One One Onto Miscellaneous




Ex 5 2 9 Prove That F X X 1 Is Not Differentiable
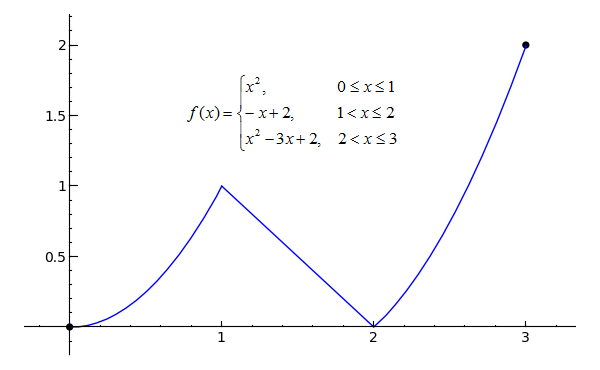



Sage Calculus Tutorial Continuity



No comments:
Post a Comment